Toom Cook
Small Field
Sumcheck
🤝🏻
Toom Cook Multiplication: Example
6219
\times \ 4418
= \ 62 \textcolor{lightgrey}{\times 10^2} + 19
= \ 44 \textcolor{lightgrey}{\times 10^2} + 18
\implies p(x)= \ 62 \textcolor{lightgrey}{\times x} + 19
\implies q(x)= \ 44 \textcolor{lightgrey}{\times x} + 18
m(x)= p(x) \cdot q(x)
\implies m(10^2)
\begin{aligned}
p(0) &= 62 \textcolor{lightgrey}{\cdot 0} + 19 = \textcolor{red}{19} \\
p(1) &= 62 \textcolor{lightgrey}{\cdot 1} + 19 = \textcolor{red}{81} \\
p(\infty) &= 62 \textcolor{lightgrey}{\cdot \small \frac{1}{0}} + 19 = \textcolor{red}{62}
\end{aligned}
\begin{aligned}
q(0) &= 44 \textcolor{lightgrey}{\cdot 0} + 18 = \textcolor{red}{18} \\
q(1) &= 44 \textcolor{lightgrey}{\cdot 1} + 18 = \textcolor{red}{62} \\
q(\infty) &= 44 \textcolor{lightgrey}{\cdot \small \frac{1}{0}} + 18 = \textcolor{red}{44}
\end{aligned}
\implies m(x)= \ 2728 \textcolor{lightgrey}{\times x^2} + 1952 \textcolor{lightgrey}{\times x} + 342
\begin{pmatrix}
1 & 0 & 0\\
1 & 1 & 1\\
0 & 0 & 1
\end{pmatrix}^{-1}
\begin{pmatrix}
342\\
5022\\
2728
\end{pmatrix}
=
\begin{pmatrix}
342\\
1952\\
2728
\end{pmatrix}
\begin{aligned}
m(0) &= 342\\
\implies \quad m(1) &= 5022\\
m(\infty) &= 2728
\end{aligned}
Toom Cook Multiplication for \(d\)
\underbrace{(p_0 + p_1\cdot x)(q_0 + q_1\cdot x)(r_0 + r_1\cdot x)\dots (y_0 + y_1\cdot x)}_{d \text{ terms}}
- Multiplying \(d\) terms each of degree \(1\) results in \((d+1)\) Toom-Cook ops
\begin{bmatrix}
p(0) \cdot q(0) \cdot r(0) \dots y(0) \\
p(1) \cdot q(1) \cdot r(1) \dots y(1) \\
p(-1) \cdot q(-1) \cdot r(-1) \dots y(-1) \\
\vdots \\
p(\infty) \cdot q(\infty) \cdot r(\infty) \dots y(\infty)
\end{bmatrix}
\underbrace{\hspace{4cm}}
(d+1)
\underbrace{\hspace{8.4cm}}
(d-1) \textsf{ bb} \text{ mults}
- Naively, we need \((d-1) \textsf{bb}\) multiplications per Toom-Cook operation
- In total, we perform \((d+1)(d-1) \textsf{bb}\) multiplications
\underbrace{(p_0 + p_1\cdot x)(q_0 + q_1\cdot x)(r_0 + r_1\cdot x)\dots (y_0 + y_1\cdot x)}_{d \text{ terms}}
- Inversion matrices can contain rational terms
- Problem: multiplying by rational factors is not good
- Solution: the prover and verifier can agree on certain scaling factors to avoid any rational multiplicands
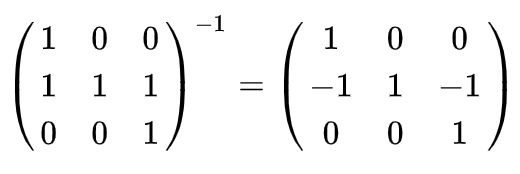
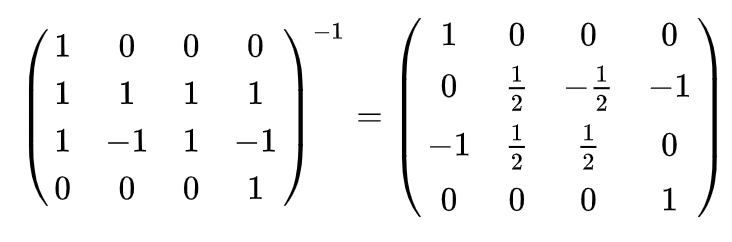


d=2
d=3
d=4
d=2
d=3
d=4
p(x)q(x)
\textcolor{red}{2}\cdot p(x)q(x)r(x)
\textcolor{red}{6}\cdot p(x)q(x)r(x)s(x)
Toom Cook Multiplication for \(d\)
Recall - Algorithm \(3\)
r_i(0) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, \dots, \alpha_{i-1}, 0, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, \dots, \alpha_{i-1}, 0, \mathbf{X})
r_1(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(c, \mathbf{X})\cdot
\textcolor{red}{b}(c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X}) +
c \cdot \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})
\Big)
\Big(
\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X}) +
c \cdot \textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
\bar{c}^2\cdot \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X})
+c^2\cdot \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
+\bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
+\bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X})
\Big)
\underbrace{\hspace{3.6cm}}
\underbrace{\hspace{3.6cm}}
\underbrace{\hspace{3.6cm}}
\underbrace{\hspace{3.6cm}}
Pre-compute with \(4\times \frac{n}{2} \ \textsf{bb}\)
+ \bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X})
+\bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
-\bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X})
-\bar{c}c \cdot\textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
(\bar{c}^2 - \bar{c}c)\cdot \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X})
+(\bar{c}^2 - \bar{c}c)\cdot \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
+\bar{c}c \cdot \left( \textcolor{blue}{a}(\textcolor{green}{0},\mathbf{X}) + \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X}) \right)
\left( \textcolor{red}{b}(\textcolor{green}{0},\mathbf{X}) + \textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X}) \right)
\Big)
\underbrace{\hspace{3.6cm}}
\underbrace{\hspace{3.6cm}}
\underbrace{\hspace{9.6cm}}
Pre-compute with \(3\times \frac{n}{2} \ \textsf{bb}\)
\begin{bmatrix}
0\cdot 0 & 0\cdot 1 \\
1\cdot 0 & 1\cdot 1
\end{bmatrix}
\(\implies\) Karatsuba trick!
Toom Cook in Sumcheck
r_1(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(c, \mathbf{X})\cdot
\textcolor{red}{b}(c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X}) +
c \cdot \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})
\Big)
\Big(
\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X}) +
c \cdot \textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X})$}
\right)
\underbrace{\hspace{3.8cm}}_{p(c) = \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X}) + c
\cdot (\textcolor{blue}{a}(\textcolor{green}{1}, \mathbf{X}) - \textcolor{blue}{a}(\textcolor{green}{0}, \mathbf{X}))}
\underbrace{\hspace{3.8cm}}_{q(c) = \textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X}) + c
\cdot (\textcolor{red}{b}(\textcolor{green}{1}, \mathbf{X}) - \textcolor{red}{b}(\textcolor{green}{0}, \mathbf{X}))}
\(\implies 3 \cdot \textsf{bb}\) multiplications
Round 1:
Toom Cook in Sumcheck
Round 2:
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
= \sum_{\mathbf{X}}
\Big( L_{1, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
+
Toom Cook in Sumcheck
Round 2:
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
= \sum_{\mathbf{X}}
\Big( L_{1, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
+
L_{2, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
Toom Cook in Sumcheck
Round 2:
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
= \sum_{\mathbf{X}}
\Big( L_{1, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
+
L_{2, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
Toom Cook in Sumcheck
Round 2:
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
= \sum_{\mathbf{X}}
\Big( L_{1, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
+
L_{2, \vec{\alpha}_1}^2 \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
\Big)
\textsf{TC2}(a_1b_2) +
\textsf{TC2}(a_2b_1) =
\textsf{TC2}((a_1 + a_2)(b_1+b_2)) -
\textsf{TC2}(a_1b_1) -
\textsf{TC2}(a_2b_2)
Toom Cook in Sumcheck
Round 2:
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{a}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{b}(\alpha_1, c, \mathbf{X})
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
L_{2, \vec{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\Big)
= \sum_{\mathbf{X}}
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
\Big(
L_{1, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})) +
L_{2, \vec{\alpha}_1} \cdot (\bar{c} \cdot \textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}) + c \cdot \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X}))
\Big)
= \sum_{\mathbf{X}}
\Big(
\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{0, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{0, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{0, 1}, \mathbf{X})$}
\right)
+
\left( L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{blue}{a}(\textcolor{green}{1, 1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{1, 0}, \mathbf{X}), \textcolor{red}{b}(\textcolor{green}{1, 1}, \mathbf{X})$}
\right)
+
L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{a}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{a}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{a}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{a}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{b}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{b}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{b}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{b}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
\Big)
\textsf{TC2}(a_1b_2) +
\textsf{TC2}(a_2b_1) =
\textsf{TC2}((a_1 + a_2)(b_1+b_2)) -
\textsf{TC2}(a_1b_1) -
\textsf{TC2}(a_2b_2)
Toom Cook for \(d=3\)
r_1(c) = \sum_{\mathbf{X}} \textcolor{blue}{p}(c, \mathbf{X})\cdot
\textcolor{red}{q}(c, \mathbf{X}) \cdot
\textcolor{orange}{r}(c, \mathbf{X})
Round 1:
= \sum_{\mathbf{X}}
\big(
L_{1, c} \cdot \textcolor{blue}{p}_{\textcolor{green}{0}} +
L_{2, c} \cdot \textcolor{blue}{p}_{\textcolor{green}{1}}
\big)
\big(
L_{1, c} \cdot \textcolor{red}{q}_{\textcolor{green}{0}} +
L_{2, c} \cdot \textcolor{red}{q}_{\textcolor{green}{1}}
\big)
\big(
L_{1, c} \cdot \textcolor{orange}{r}_{\textcolor{green}{0}} +
L_{2, c} \cdot \textcolor{orange}{r}_{\textcolor{green}{1}}
\big)
= \sum_{\mathbf{X}}
\textsf{TC}_{3, 2}(p, q, r)
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{p}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{q}(\alpha_1, c, \mathbf{X}) \cdot
\textcolor{orange}{r}(\alpha_1, c, \mathbf{X})
Round 2:
= \sum_{\mathbf{X}}
\big(
L_{1, \alpha_1} \cdot \textcolor{blue}{p}_{\textcolor{green}{0}}(c) +
L_{2, \alpha_1} \cdot \textcolor{blue}{p}_{\textcolor{green}{1}}(c)
\big)
\big(
L_{1, \alpha_1} \cdot \textcolor{red}{q}_{\textcolor{green}{0}}(c) +
L_{2, \alpha_1} \cdot \textcolor{red}{q}_{\textcolor{green}{1}}(c)
\big)
\big(
L_{1, \alpha_1} \cdot \textcolor{orange}{r}_{\textcolor{green}{0}}(c) +
L_{2, \alpha_1} \cdot \textcolor{orange}{r}_{\textcolor{green}{1}}(c)
\big)
= \sum_{\mathbf{X}}
\textsf{TC}_{3, 2}(p', q', r')
- How do we optimally compute \(\textsf{TC}_{3, 2}\)?
Toom Cook Optimisation for \(d=3\)
r_1(c) = \sum_{\mathbf{X}} \textcolor{blue}{p}(c, \mathbf{X})\cdot
\textcolor{red}{q}(c, \mathbf{X}) \cdot
\textcolor{orange}{r}(c, \mathbf{X})
Round 1:
= \sum_{\mathbf{X}}
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{0}, \mathbf{X}), \textcolor{blue}{p}(\textcolor{green}{1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{0}, \mathbf{X}), \textcolor{red}{q}(\textcolor{green}{1}, \mathbf{X})$}
\right)
\cdot \textcolor{orange}{r}(c, \mathbf{X})
= \sum_{\mathbf{X}}
\textsf{TC2.5}_{c}
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{0}, \mathbf{X}), \textcolor{blue}{p}(\textcolor{green}{1}, \mathbf{X})$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{0}, \mathbf{X}), \textcolor{red}{q}(\textcolor{green}{1}, \mathbf{X})$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{0}, \mathbf{X}), \textcolor{orange}{r}(\textcolor{green}{1}, \mathbf{X})$}
\right)
\(\implies \textsf{TC2} \longrightarrow 3 \cdot \textsf{bb}\) multiplications
\(\implies \textsf{TC2.5} \longrightarrow 4 \cdot \textsf{bb}\) multiplications
\(\implies\) Total requires \(7 \cdot \textsf{bb}\) multiplications
\(\implies\) JT's method requires \(14 \cdot \textsf{bb}\) multiplications
r_2(c) = \sum_{\mathbf{X}} \textcolor{blue}{p}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{q}(\alpha_1, c, \mathbf{X}) \cdot
\textcolor{orange}{r}(\alpha_1, c, \mathbf{X})
\textcolor{blue}{p}(\alpha_1, c, \mathbf{X})\cdot
\textcolor{red}{q}(\alpha_1, c, \mathbf{X})
=
\textcolor{skyblue}{\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right)}
\cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left(L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1}\right)}
\cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1}}
\cdot
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
\textcolor{orange}{r}(\alpha_1, c, \mathbf{X})
=
L_{1, \vec{\alpha}_1}
(
\bar{c} \cdot \textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot) +
c \cdot \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot))
+
L_{2, \vec{\alpha}_1}
(
\bar{c} \cdot \textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot) +
c \cdot \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot))
\textcolor{blue}{p}(*)\cdot
\textcolor{red}{q}(*)\cdot
\textcolor{orange}{r}(*)
=
\textcolor{skyblue}{\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right)L_{1, \vec{\alpha}_1}}
\cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left( L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) L_{1, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1}^2 L_{2, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right)L_{2, \vec{\alpha}_1}}
\cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left( L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) L_{2, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1} L_{2, \vec{\alpha}_1}^2} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
Toom Cook Optimisation for \(d=3\)
\textcolor{blue}{p}(*)\cdot
\textcolor{red}{q}(*)\cdot
\textcolor{orange}{r}(*)
=
\textcolor{skyblue}{\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right)L_{1, \vec{\alpha}_1}}
\cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left( L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) L_{1, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1}^2 L_{2, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left(L_{1, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right)L_{2, \vec{\alpha}_1}}
\cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
+
\textcolor{skyblue}{\left( L_{2, \vec{\alpha}_1}^2 - L_{1, \vec{\alpha}_1}L_{2, \vec{\alpha}_1} \right) L_{2, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1} L_{2, \vec{\alpha}_1}^2} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
\textcolor{blue}{p}(*)\cdot
\textcolor{red}{q}(*)\cdot
\textcolor{orange}{r}(*)
=
\textcolor{skyblue}{L_{1, \vec{\alpha}_1}^3}
\cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
+
\textcolor{skyblue}{L_{1, \vec{\alpha}_1}^2 L_{2, \vec{\alpha}_1}} \cdot
\textsf{TC2.5}_c
\left(
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot),
\textcolor{blue}{p}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{0}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot),
\textcolor{red}{q}(\textcolor{green}{\underline{1}}, \cdot) + \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right),
\fcolorbox{red}{none}{$\textcolor{orange}{r}(\textcolor{green}{\underline{0}}, \cdot), \textcolor{orange}{r}(\textcolor{green}{\underline{1}}, \cdot)$}
\right)
-
\textsf{TC2}_c
\left(
\fcolorbox{blue}{none}{$\textcolor{blue}{p}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{blue}{p}(\textcolor{green}{\underline{3}}, \cdot)$},
\fcolorbox{red}{none}{$\textcolor{red}{q}(\textcolor{green}{\underline{2}}, \cdot), \textcolor{red}{q}(\textcolor{green}{\underline{3}}, \cdot)$}
\right)
\(\implies\) Total requires \(28 \cdot \textsf{bb}\) multiplications
\(\implies\) JT's method requires \(52 \cdot \textsf{bb}\) multiplications
\implies 7 \cdot 2^{i-1}
\implies (2^{i-1} + 4^i - 4^{i-1})
Toom Cook Optimisation for \(d=3\)
Comparison for \(d=2\) and \(d=3\)
\begin{aligned}
G_2(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X})
=&\
\textcolor{blue}{a}(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X})\cdot
\textcolor{red}{b}(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X}) \\[4pt]
=&\
\big(
\textcolor{skyblue}{\bar{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
\textcolor{skyblue}{\alpha_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\big)
\big(
\textcolor{skyblue}{\bar{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
\textcolor{skyblue}{\alpha_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\big) \\[4pt]
=&\ \textcolor{skyblue}{\bar{\alpha}_1^2} \cdot \textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}} + \\[2pt]
&\ \textcolor{skyblue}{\alpha_1^2} \cdot \textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} + \\[2pt]
&\ \textcolor{skyblue}{\bar{\alpha}_1\alpha_1} \cdot \textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} + \\[2pt]
&\ \textcolor{skyblue}{\bar{\alpha}_1\alpha_1} \cdot \textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}}
\end{aligned}
\begin{aligned}
G_2(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X})
=&\
\textcolor{blue}{a}(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X})\cdot
\textcolor{red}{b}(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X}) \cdot
\textcolor{orange}{c}(\textcolor{skyblue}{\alpha_1}, c, \mathbf{X})\\[4pt]
=&\
\big(
\textcolor{skyblue}{\bar{\alpha}_1} \cdot \textcolor{blue}{a}(\textcolor{green}{0}, c, \mathbf{X}) +
\textcolor{skyblue}{\alpha_1} \cdot \textcolor{blue}{a}(\textcolor{green}{1}, c, \mathbf{X})
\big)
\big(
\textcolor{skyblue}{\bar{\alpha}_1} \cdot \textcolor{red}{b}(\textcolor{green}{0}, c, \mathbf{X}) +
\textcolor{skyblue}{\alpha_1} \cdot \textcolor{red}{b}(\textcolor{green}{1}, c, \mathbf{X})
\big)
\big(
\textcolor{skyblue}{\bar{\alpha}_1} \cdot \textcolor{orange}{c}(\textcolor{green}{0}, c, \mathbf{X}) +
\textcolor{skyblue}{\alpha_1} \cdot \textcolor{orange}{c}(\textcolor{green}{1}, c, \mathbf{X})
\big)\\[4pt]
=&\ \textcolor{skyblue}{\bar{\alpha}_1^3} \cdot \textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}} \cdot \textcolor{orange}{c}_{\textcolor{green}{0}} \ + \\[2pt]
&\ \textcolor{skyblue}{\alpha_1^3} \cdot \textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} \cdot \textcolor{orange}{c}_{\textcolor{green}{1}} \ + \\[2pt]
&\ \textcolor{skyblue}{\bar{\alpha}_1^2\alpha_1} \cdot
\Big(
\textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} \cdot \textcolor{orange}{c}_{\textcolor{green}{0}} \ + \
\textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}} \cdot \textcolor{orange}{c}_{\textcolor{green}{0}} \ + \
\textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}} \cdot \textcolor{orange}{c}_{\textcolor{green}{1}}
\Big) + \\[2pt]
&\ \textcolor{skyblue}{\bar{\alpha}_1\alpha_1^2} \cdot
\Big(
\textcolor{blue}{a}_{\textcolor{green}{0}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} \cdot \textcolor{orange}{c}_{\textcolor{green}{1}} \ + \
\textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{0}} \cdot \textcolor{orange}{c}_{\textcolor{green}{1}} \ + \
\textcolor{blue}{a}_{\textcolor{green}{1}} \cdot \textcolor{red}{b}_{\textcolor{green}{1}} \cdot \textcolor{orange}{c}_{\textcolor{green}{0}}
\Big)
\end{aligned}