Parallelising Sumcheck
MLE Sumcheck
x_2
x_3
x_1
f(0,0,0) = f_1
f(0,0,1) = f_2
f(0,1,1) = f_4
f(0,1,0) = f_3
f(1,1,0) = f_7
f(1,1,1) = f_8
f(1,0,0) = f_5
f(1,0,1) = f_6
\begin{bmatrix}
& \\
& \\
& \\
& \\
& \\
& \\
& \\
& \\
& \\
& \\
& \\
& \\
\end{bmatrix}
\implies f(X_3, X_2, X_1)
MLE Sumcheck
f(0,0,0) = f_1
x_2
x_3
f(0,0,1) = f_2
f(0,1,1) = f_4
f(0,1,0) = f_3
f(1,1,0) = f_7
f(1,1,1) = f_8
f(1,0,0) = f_5
f(1,0,1) = f_6
x_1
- MLE representation makes sumcheck prover's computation parallelisable
- Computing round polynomials is easy
r_1(X) := (1-X)\textcolor{orange}{\sum_{x_2, x_1} f(0, x_2, x_1)}
+ X\textcolor{93c47d}{\sum_{x_2, x_1} f(1, x_2, x_1)}
- Need to fold along a dimension each round
\alpha_3
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
\alpha_3
\alpha_3
\alpha_3
MLE Sumcheck
f_1
x_2
x_3
f_2
f_4
f_3
f_7
f_8
f_5
f_6
x_1
- MLE representation makes sumcheck prover's computation parallelisable
- Computing round polynomials is easy
r_1(X) := (1-X)\textcolor{orange}{\sum_{x_2, x_1} f(0, x_2, x_1)}
+ X\textcolor{93c47d}{\sum_{x_2, x_1} f(1, x_2, x_1)}
- Need to fold along a dimension in each round
\alpha_3
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
\alpha_3
\alpha_3
\alpha_3
MLE Sumcheck
x_2
x_1
- MLE representation makes sumcheck prover's computation parallelisable
- Computing round polynomials is easy
r_1(X) := (1-X)\textcolor{orange}{\sum_{x_2, x_1} f(0, x_2, x_1)}
+ X\textcolor{93c47d}{\sum_{x_2, x_1} f(1, x_2, x_1)}
- Need to fold along a dimension in each round
f_1
f_2
f_4
f_3
f_7
f_8
f_5
f_6
+ \alpha_3
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
+ \alpha_3
+\alpha_3
+\alpha_3
r_2(X) := (1-X)\textcolor{orange}{\sum_{x_1} f(\alpha_3, 0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f(\alpha_3, 1, x_1)}
= (1-X)\textcolor{orange}{\sum_{x_1} f'_{\alpha_3}(0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f'_{\alpha_3}(1, x_1)}
MLE Sumcheck
x_2
x_1
- MLE representation makes sumcheck prover's computation parallelisable
- Computing round polynomials is easy
r_1(X) := (1-X)\textcolor{orange}{\sum_{x_2, x_1} f(0, x_2, x_1)}
+ X\textcolor{93c47d}{\sum_{x_2, x_1} f(1, x_2, x_1)}
- Need to fold along a dimension in each round
f_1
f_2
f_4
f_3
f_7
f_8
f_5
f_6
+ \alpha_3
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
+ \alpha_3
+\alpha_3
+\alpha_3
r_2(X) := (1-X)\textcolor{orange}{\sum_{x_1} f(\alpha_3, 0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f(\alpha_3, 1, x_1)}
= (1-X)\textcolor{orange}{\sum_{x_1} f'_{\alpha_3}(0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f'_{\alpha_3}(1, x_1)}
(1-\alpha_2)
\alpha_2
(1-\alpha_2)
(1-\alpha_2)
(1-\alpha_2)
\alpha_2
\alpha_2
\alpha_2
MLE Sumcheck
x_1
- MLE representation makes sumcheck prover's computation parallelisable
- Computing round polynomials is easy
r_1(X) := (1-X)\textcolor{orange}{\sum_{x_2, x_1} f(0, x_2, x_1)}
+ X\textcolor{93c47d}{\sum_{x_2, x_1} f(1, x_2, x_1)}
- Need to fold along a dimension in each round
f_1
f_2
f_4
f_3
f_7
f_8
f_5
f_6
+ \alpha_3
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
(1-\alpha_3)
+ \alpha_3
+\alpha_3
+\alpha_3
r_2(X) := (1-X)\textcolor{orange}{\sum_{x_1} f(\alpha_3, 0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f(\alpha_3, 1, x_1)}
= (1-X)\textcolor{orange}{\sum_{x_1} f'_{\alpha_3}(0, x_1)}
+ X\textcolor{93c47d}{\sum_{x_1} f'_{\alpha_3}(1, x_1)}
(1-\alpha_2)
\alpha_2
(1-\alpha_2)
(1-\alpha_2)
(1-\alpha_2)
\alpha_2
\alpha_2
\alpha_2
r_3(X) := (1-X)\textcolor{orange}{\sum_{x_1} f''_{\alpha_3, \alpha_2}(0)}
+ X\textcolor{93c47d}{\sum_{x_1} f'_{\alpha_3, \alpha_2}(1)}
- Upadting original polynomial with challenges is tricky
MLE Sumcheck
f(\mathbf{X})
f_{1,o}
f_{1,e}
\sum
\sum
\textsf{hash}
\alpha_4
f_{2,o}
f_{2,e}
\sum
\sum
\textsf{hash}
\alpha_3
f_{3,o}
f_{3,e}
\sum
\sum
\textsf{hash}
\alpha_2
f_{4,o}
f_{4,e}
\sum
\sum
\textsf{hash}
\alpha_1
Round computation can be parallelised
Round \(i+1\) depends on round \(i\) challenge
Need to process all terms to compute challenge
Sumcheck as a Backend
- For R1CS arithmetisation [1]:
\begin{bmatrix}
\\
& \bar{A} & \\
\\
\end{bmatrix}
\hspace{-6pt}
\begin{bmatrix}
\\
\vec{z}\\
\\
\end{bmatrix}
\circ
\begin{bmatrix}
\\
& \bar{B} & \\
\\
\end{bmatrix}
\hspace{-6pt}
\begin{bmatrix}
\\
\vec{z}\\
\\
\end{bmatrix}
=
\begin{bmatrix}
\\
& \bar{C} & \\
\\
\end{bmatrix}
\hspace{-6pt}
\begin{bmatrix}
\\
\vec{z}\\
\\
\end{bmatrix}
G(x) := \left(\Bigg(\sum_{y \in \mathbb{B}_\mu}A(x,y)z(y)\Bigg)\Bigg(\sum_{y \in \mathbb{B}_\mu}B(x,y)z(y)\Bigg) - \sum_{y \in \mathbb{B}_\mu}C(x,y)z(y)\right)
\textcolor{orange}{\textsf{eq}(x, \tau)}
- For Plonkish arithmetisation [2]:
\sum_{x} a(x)b(x)\textsf{eq}(x) - c(x)\textsf{eq}(x) = 0
\begin{aligned}
& \textcolor{grey}{S_{\textsf{add}}(\vec{x})}
\Big( \textcolor{red}{L(\vec{x})} + \textcolor{94c47d}{R(\vec{x})} \Big)
+
\textcolor{grey}{S_{\textsf{mul}}(\vec{x})}
\Big(\textcolor{red}{L(\vec{x})} \cdot \textcolor{94c47d}{R(\vec{x})}\Big)
+
& \textcolor{grey}{S_{\textsf{gate}}(\vec{x})}
G\Big[ \textcolor{red}{L(\vec{x})}, \textcolor{94c47d}{R(\vec{x})} \Big]
- \textcolor{skyblue}{O(\vec{x})} = 0
\end{aligned}
- Sumcheck can work as a proof system and arithmetisation agnostic backend
\textsf{combine}_{\text{R1CS}}(a,b,c,d) := abd - cd
\textsf{combine}_{\text{plonkish}}(a,b,c, s_1, s_2, s_3) := s_1(a + b) + s_2 ab + s_3 G(a, b) - c
MLE Sumcheck Round
f_{1,o}
f_{1,e}
\sum
\sum
\textsf{hash}
\alpha_i
s = \sum_{\vec{x}}f(\vec{x})
s = \sum_{\vec{x}}p(\vec{x}) q(\vec{x})
L(c)
\hspace{1cm}
f_1
L(c)
\hspace{1cm}
f_2
L(c)
\hspace{1cm}
f_3
L(c)
\hspace{1cm}
f_4
L(c)
\hspace{1cm}
f_5
L(c)
\hspace{1cm}
f_6
L(c)
\hspace{1cm}
f_7
L(c)
\hspace{1cm}
f_8
L(c)
\hspace{1cm}
g_1
L(c)
\hspace{1cm}
g_2
L(c)
\hspace{1cm}
g_3
L(c)
\hspace{1cm}
g_4
L(c)
\hspace{1cm}
g_5
L(c)
\hspace{1cm}
g_6
L(c)
\hspace{1cm}
g_7
L(c)
\hspace{1cm}
g_8
\textsf{combine}(f,g)
r_i(c)
\begin{bmatrix}
& & \\
& & \\
& & \\
& & \\
\end{bmatrix}_{c \in [d]}
\textsf{hash}
\alpha_i
Challenges
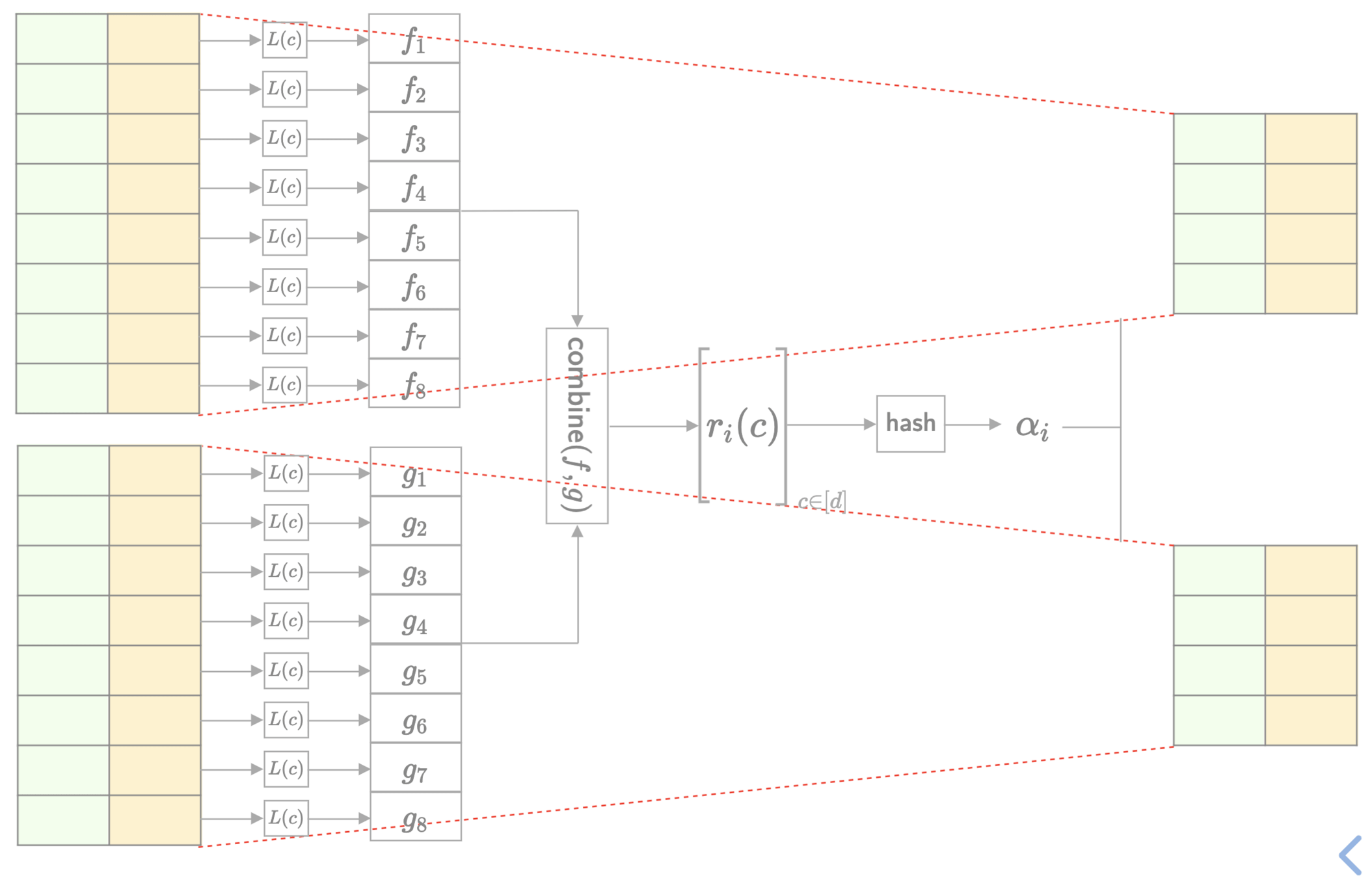
- Step 1: Linearisation is parallelisable
- Step 2: \(\textsf{combine}\) is parallelisable
- Step 3: \(\textsf{hash}\) needs all \(\{r_i(c)\}_{c \in \{0,1,\dots, d-1\}}\)
- Step 4: Folding of state is parallelisable
- Memory constraints
- RTX 4090 can fit one instance of \(2^{19}\) R1CS
- For larger sizes, break the computation down in chunks of size \(2^{19}\)
- Reads: All witness data will be read twice to L2 cache
- Writes: Updates in first few round will need to written back to memory
- Challenge computation depends on the entire witness state
- Can we perform "look-ahead" computation instead of waiting for challenges?
The Good
The Bad
Witness-Challenge Separation

[1] Justin Thaler, The Sum-Check Protocol over Fields of Small Characteristic, 2023
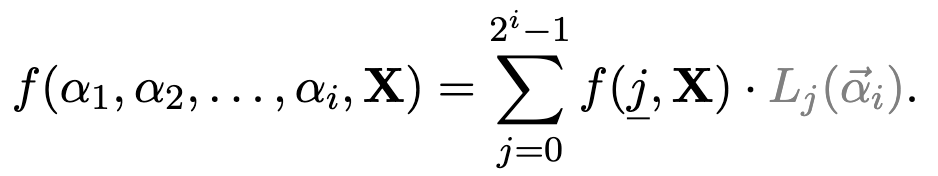
\implies
f(\alpha_1, \alpha_2, \dots, \alpha_i, \mathbf{X}) =
\textcolor{d089ff}{(1-\alpha_1)}f(\textcolor{pink}{0}, \alpha_2, \dots, \alpha_i, \mathbf{X})
\textcolor{d089ff}{(1-\alpha_1)(1-\alpha_2)}f(\textcolor{pink}{0, 0}, \alpha_3, \dots, \alpha_i, \mathbf{X})
+ \textcolor{d089ff}{(\alpha_1)}f(\textcolor{pink}{1}, \alpha_2, \dots, \alpha_i, \mathbf{X})
+
\textcolor{d089ff}{(1-\alpha_1)(\alpha_2)}f(\textcolor{pink}{0, 1}, \alpha_3, \dots, \alpha_i, \mathbf{X})
+\textcolor{d089ff}{(\alpha_1)(1-\alpha_2)}f(\textcolor{pink}{1, 0}, \alpha_3, \dots, \alpha_i, \mathbf{X})
+
\textcolor{d089ff}{(\alpha_1)(\alpha_2)}f(\textcolor{pink}{1, 1}, \alpha_3, \dots, \alpha_i, \mathbf{X})
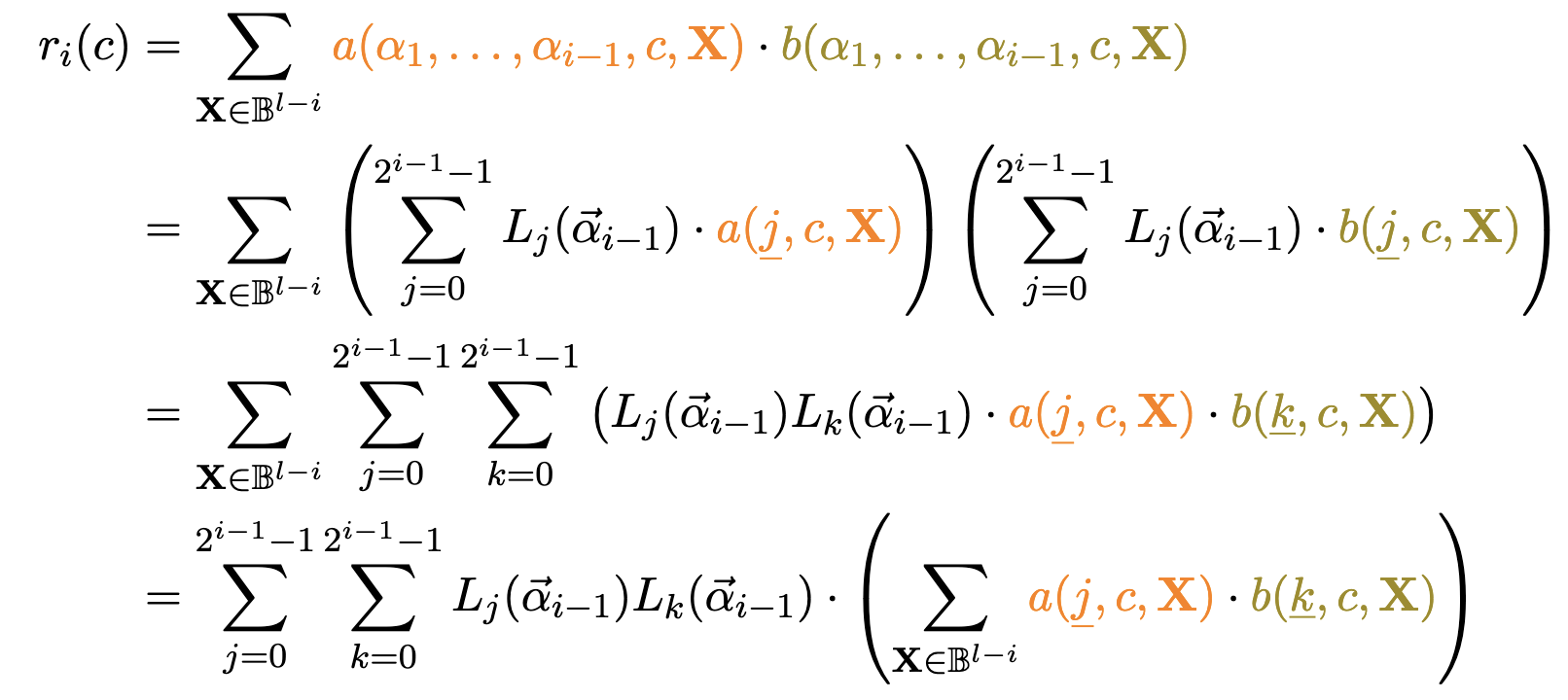
\therefore
Witness-Challenge Separation
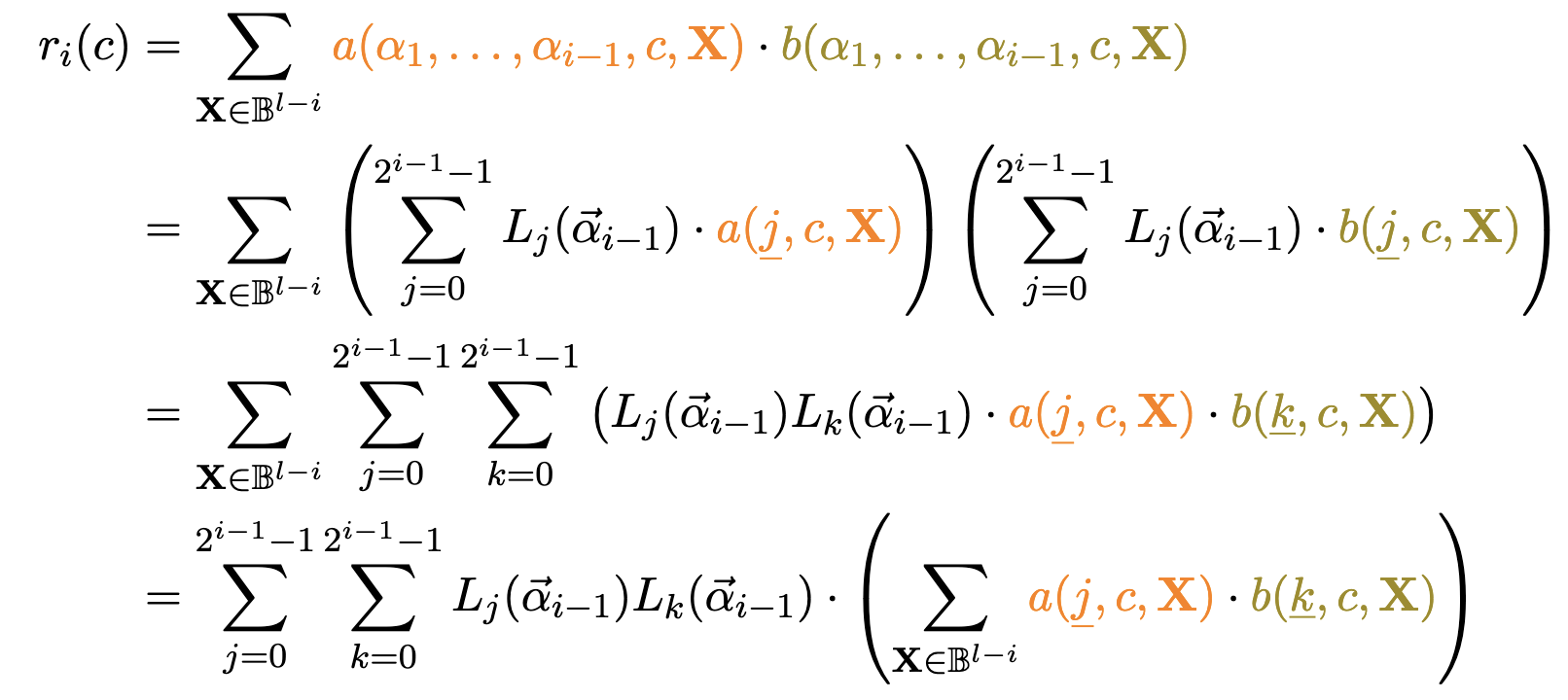
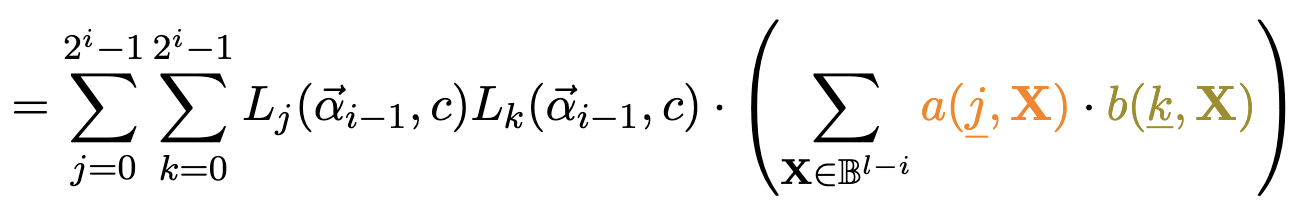
\underbrace{\hspace{5.8cm}}{}
Challenge term
\underbrace{\hspace{6cm}}{}
Witness term
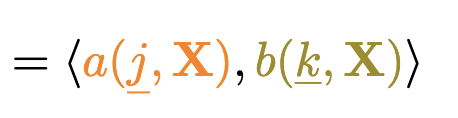
Witness-Challenge Separation
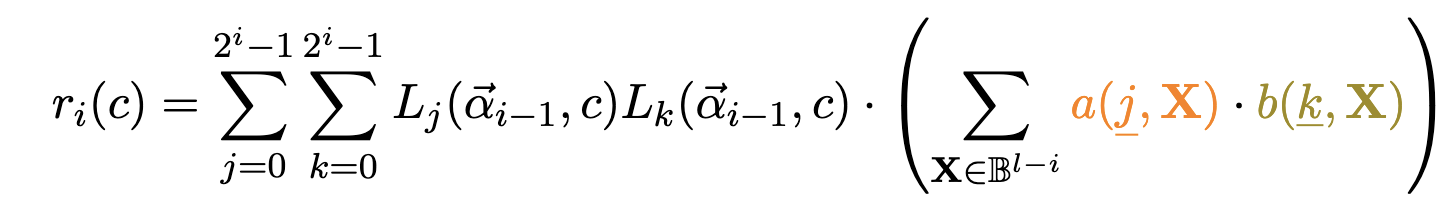
\begin{bmatrix}
& & & & & & & & & & & & & & & & \\
\end{bmatrix}_{1 \times 2^i}
L_1(\vec{\alpha}_i)
L_2(\vec{\alpha}_i)
L_3(\vec{\alpha}_i)
L_{2^i}(\vec{\alpha}_i)
\dots
\begin{bmatrix}
& & \\
& & \\
& & \\
& & \\
& & \\
& & \\
& & \\
& & \\
& & \\
\end{bmatrix}_{2^{i} \times 1}
L_1(\vec{\alpha}_i)
L_2(\vec{\alpha}_i)
L_3(\vec{\alpha}_i)
\vdots
L_{2^i}(\vec{\alpha}_i)
\boxdot
\begin{bmatrix}
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
& & & & & & \\
\end{bmatrix}_{2^{i} \times \frac{n}{2^i}}
a(\underline{0}, \mathbf{X})
a(\underline{1}, \mathbf{X})
a(\underline{2}, \mathbf{X})
a(\underline{\small 2^i-1}, \mathbf{X})
\vdots
b(\underline{0}, \mathbf{X})
b(\underline{1}, \mathbf{X})
b(\underline{\small 2^{i}-1}, \mathbf{X})
\dots
\begin{bmatrix}
& & & & & & & & & & & & & & & & \\
& & & & & & & & & & & & & & & & \\
& & & & & & & & & & & & & & & & \\
& & & & & & & & & & & & & & & & \\
\end{bmatrix}_{\frac{n}{2^i} \times 2^i}
- Matrix operations faster on GPU
- We can generalise this to any sumcheck instance
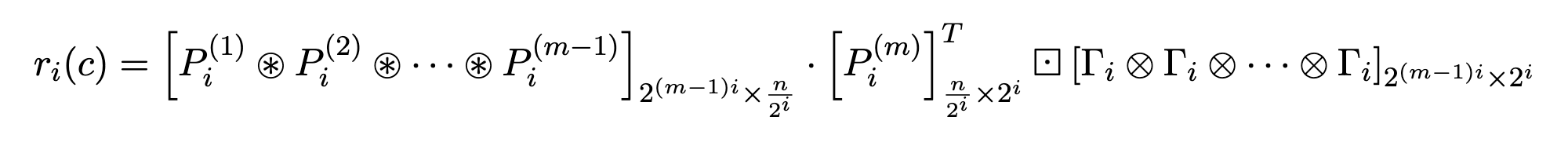
a_1
a_2
a_3
a_4
a_5
a_6
a_7
a_8
a_9
a_{10}
a_{11}
a_{12}
a_{13}
a_{14}
a_{15}
a_{16}
{\scriptsize \sum}_{1}^{8}
{\scriptsize \sum}_{9}^{16}
{\scriptsize \sum}_{1}^{4}
{\scriptsize \sum}_{9}^{12}
{\scriptsize \sum}_{5}^{8}
{\scriptsize \sum}_{13}^{16}
{\scriptsize \sum}_{1}^{2}
{\scriptsize \sum}_{9}^{10}
{\scriptsize \sum}_{3}^{4}
{\scriptsize \sum}_{11}^{12}
{\scriptsize \sum}_{5}^{6}
{\scriptsize \sum}_{13}^{14}
{\scriptsize \sum}_{7}^{8}
{\scriptsize \sum}_{15}^{16}
\ a_1 \
\hspace{1.4mm} a_9 \hspace{1.5mm}
\ a_2 \
\hspace{0.88mm} a_{10} \hspace{0.88mm}
\ a_3 \
\hspace{0.88mm} a_{11} \hspace{0.88mm}
\ a_4 \
\hspace{0.88mm} a_{12} \hspace{0.88mm}
\ a_5 \
\hspace{0.88mm} a_{13} \hspace{0.88mm}
\ a_6 \
\hspace{0.88mm} a_{14} \hspace{0.88mm}
\ a_7 \
\hspace{0.88mm} a_{15} \hspace{0.88mm}
\ a_8 \
\hspace{0.88mm} a_{16} \hspace{0.88mm}
\odot
\textsf{hash}
1
1
\bar{\alpha}_1
\bar{\alpha}_1
\alpha_1
\alpha_1
\bar{\alpha}_1\bar{\alpha}_2
\bar{\alpha}_1
\alpha_2
\alpha_1
\bar{\alpha}_2
\alpha_1
\alpha_2
\bar{\alpha}_1\bar{\alpha}_2
\bar{\alpha}_1
\alpha_2
\alpha_1
\bar{\alpha}_2
\alpha_1
\alpha_2
\bar{\alpha}_1\bar{\alpha}_2\bar{\alpha}_3
\bar{\alpha}_1
\alpha_2
\bar{\alpha}_3
\alpha_1
\bar{\alpha}_2\bar{\alpha}_3
\alpha_1
\alpha_2
\alpha_3
\bar{\alpha}_1\bar{\alpha}_2
\alpha_3
\bar{\alpha}_1
\alpha_2
\alpha_3
\alpha_1
\bar{\alpha}_2
\alpha_3
\alpha_1
\alpha_2
\bar{\alpha}_3
\bar{\alpha}_1\bar{\alpha}_2\bar{\alpha}_3
\bar{\alpha}_1
\alpha_2
\bar{\alpha}_3
\alpha_1
\bar{\alpha}_2\bar{\alpha}_3
\alpha_1
\alpha_2
\alpha_3
\bar{\alpha}_1\bar{\alpha}_2
\alpha_3
\bar{\alpha}_1
\alpha_2
\alpha_3
\alpha_1
\bar{\alpha}_2
\alpha_3
\alpha_1
\alpha_2
\bar{\alpha}_3
\odot
\textsf{hash}
\odot
\textsf{hash}
a_1
a_2
a_3
a_4
a_5
a_6
a_7
a_8
a_9
a_{10}
a_{11}
a_{12}
a_{13}
a_{14}
a_{15}
a_{16}
{\scriptsize \sum}_{1}^{4}
{\scriptsize \sum}_{9}^{12}
{\scriptsize \sum}_{5}^{8}
{\scriptsize \sum}_{13}^{16}
{\scriptsize \sum}_{1}^{2}
{\scriptsize \sum}_{9}^{10}
{\scriptsize \sum}_{3}^{4}
{\scriptsize \sum}_{11}^{12}
{\scriptsize \sum}_{5}^{6}
{\scriptsize \sum}_{13}^{14}
{\scriptsize \sum}_{7}^{8}
{\scriptsize \sum}_{15}^{16}
\bar{\alpha}_1
\bar{\alpha}_1
\alpha_1
\alpha_1
\bar{\alpha}_1\bar{\alpha}_2
\bar{\alpha}_1
\alpha_2
\alpha_1
\bar{\alpha}_2
\alpha_1
\alpha_2
\bar{\alpha}_1\bar{\alpha}_2
\bar{\alpha}_1
\alpha_2
\alpha_1
\bar{\alpha}_2
\alpha_1
\alpha_2
\bar{\alpha}_1\bar{\alpha}_2\bar{\alpha}_3
\bar{\alpha}_1
\alpha_2
\bar{\alpha}_3
\alpha_1
\bar{\alpha}_2\bar{\alpha}_3
\alpha_1
\alpha_2
\alpha_3
\bar{\alpha}_1\bar{\alpha}_2
\alpha_3
\bar{\alpha}_1
\alpha_2
\alpha_3
\alpha_1
\bar{\alpha}_2
\alpha_3
\alpha_1
\alpha_2
\bar{\alpha}_3
\bar{\alpha}_1\bar{\alpha}_2\bar{\alpha}_3
\bar{\alpha}_1
\alpha_2
\bar{\alpha}_3
\alpha_1
\bar{\alpha}_2\bar{\alpha}_3
\alpha_1
\alpha_2
\alpha_3
\bar{\alpha}_1\bar{\alpha}_2
\alpha_3
\bar{\alpha}_1
\alpha_2
\alpha_3
\alpha_1
\bar{\alpha}_2
\alpha_3
\alpha_1
\alpha_2
\bar{\alpha}_3
\odot
\textsf{hash}
\odot
\textsf{hash}
b_1
b_2
b_3
b_4
b_5
b_6
b_7
b_8
b_9
b_{10}
b_{11}
b_{12}
b_{13}
b_{14}
b_{15}
b_{16}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
{\scriptsize \dots}
Challenges
- No need to update witness state after getting a challenge
- Can reuse some computation in look-ahead computation
- Matrix operations in look-ahead computation can be faster on GPUs
The Good
- Need \(2^{i(d-1)}\) cache memory to store look-ahead witnesses in round \(i\)
- Need \(2^{i}\) cache memory to store challenges
- Memory constraints \(\implies\) use witness-separation only upto certain round
- Cannot perform look-ahead computation in a single read
- Arguably more complex algorithm and hence implementation
The Bad
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
\times
\times
\times
\times
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
\times
\times
\times
\times
\times
\times
\times
\times
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
p_0
p_1
q_0
q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
p
000
001
010
011
100
101
110
111
q
000
001
010
011
100
101
110
111
p
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
q
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
\times
f_1 =
\begin{bmatrix}
2 & 3 & 4 & 1 \\
0 & 8 & 3 & 2 \\
\end{bmatrix}
g_1 =
\begin{bmatrix}
1 & 4 & 2 & 5 \\
4 & 3 & 1 & 6 \\
\end{bmatrix}
\begin{bmatrix}
2 & 12 & 8 & 5 \\
8 & 9 & 4 & 6 \\
0 & 32 & 6 & 10 \\
0 & 24 & 3 & 12 \\
\end{bmatrix}
\circledast
\oplus
\begin{bmatrix}
27 \\
27 \\
48 \\
39 \\
\end{bmatrix}
r_1(c)
\begin{bmatrix}
\gray{(1-c)} \\
\gray{c}
\end{bmatrix}
=
\Gamma_1(c)
\begin{bmatrix*}[l]
\gray{(1-c)^2} \\
\gray{(1-c)c} \\
\gray{c(1-c)} \\
\gray{c^2}
\end{bmatrix*}
\circledast
\odot
Round 1
f_2 =
\begin{bmatrix}
2 & 3 \\
4 & 1 \\
0 & 8 \\
3 & 2 \\
\end{bmatrix}
g_2 =
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
4 & 3 \\
1 & 6 \\
\end{bmatrix}
\begin{bmatrix}
2 & 12 \\
4 & 15 \\
8 & 9 \\
2 & 18 \\
4 & 4 \\
8 & 5 \\
16 & 3 \\
4 & 6 \\
0 & 32 \\
0 & 40 \\
0 & 24 \\
0 & 48 \\
3 & 8 \\
6 & 10 \\
12 & 6 \\
3 & 12 \\
\end{bmatrix}
\circledast
\oplus
\begin{bmatrix}
14 \\
19 \\
17 \\
20 \\
8 \\
13 \\
19 \\
10 \\
32 \\
40 \\
24 \\
48 \\
11 \\
16 \\
18 \\
15 \\
\end{bmatrix}
r_2(c)
\begin{bmatrix*}[l]
\gray{(1-\alpha_1)(1-c)} \\
\gray{(1-\alpha_1)c} \\
\gray{\alpha_1(1-c)} \\
\gray{\alpha_1c}
\end{bmatrix*}
=
\Gamma_2(c)
\begin{bmatrix*}[l]
\gray{(1-\alpha_1)^2(1-c)^2} \\
\gray{(1-\alpha_1)^2(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1(1-c)^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)^2(1-c)c} \\
\gray{(1-\alpha_1)^2c^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1c^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{\alpha_1^2(1-c)^2} \\
\gray{\alpha_1^2(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1c^2} \\
\gray{\alpha_1^2(1-c)c} \\
\gray{\alpha_1^2c^2} \\
\end{bmatrix*}
\circledast
\odot
Round 2
f_2 =
\begin{bmatrix}
2 & 3 \\
4 & 1 \\
0 & 8 \\
3 & 2 \\
\end{bmatrix}
g_2 =
\begin{bmatrix}
1 & 4 \\
2 & 5 \\
4 & 3 \\
1 & 6 \\
\end{bmatrix}
\begin{bmatrix}
2 & 12 \\
4 & 15 \\
8 & 9 \\
2 & 18 \\
4 & 4 \\
8 & 5 \\
16 & 3 \\
4 & 6 \\
0 & 32 \\
0 & 40 \\
0 & 24 \\
0 & 48 \\
3 & 8 \\
6 & 10 \\
12 & 6 \\
3 & 12 \\
\end{bmatrix}
\circledast
\oplus
\begin{bmatrix}
14 \\
19 \\
17 \\
20 \\
8 \\
13 \\
19 \\
10 \\
32 \\
40 \\
24 \\
48 \\
11 \\
16 \\
18 \\
15 \\
\end{bmatrix}
r_2(c)
\begin{bmatrix*}[l]
\gray{(1-\alpha_1)(1-c)} \\
\gray{(1-\alpha_1)c} \\
\gray{\alpha_1(1-c)} \\
\gray{\alpha_1c}
\end{bmatrix*}
=
\Gamma_2(c)
\begin{bmatrix*}[l]
\gray{(1-\alpha_1)^2(1-c)^2} \\
\gray{(1-\alpha_1)^2(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1(1-c)^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)^2(1-c)c} \\
\gray{(1-\alpha_1)^2c^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1c^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)^2} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{\alpha_1^2(1-c)^2} \\
\gray{\alpha_1^2(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1(1-c)c} \\
\gray{(1-\alpha_1)\alpha_1c^2} \\
\gray{\alpha_1^2(1-c)c} \\
\gray{\alpha_1^2c^2} \\
\end{bmatrix*}
\circledast
\odot
Round 2
Memory
m \times 2^n
(2^i)^m \times 2^{n-i}
(2^i)^m
(2^i)^m
2^i
Multiplications
0
(2^i)^m \times 2^{n-i}
0
(2^i)^m
2^i
c = pq
d = cr
p
q
r
p_{0}
p_{1}
q_{0}
q_{1}
r_{0}
r_{1}
c_0 = p_0q_1
c_1 = p_1q_0
c_0 = p_0q_1
p_{00}
p_{01}
p_{10}
p_{11}
q_{00}
q_{01}
q_{10}
q_{11}
r_{00}
r_{01}
r_{10}
r_{11}
0
1
2
3
p_0
p_1
p_3
p_4
p_{16}
q_0
q_2
q_3
q_4