Jagged PCS
Journal Club
July 9 2025
zkVM Trace
Op A
Op B
2^{n_1}
2^{n_2}
Op C
2^{n_2}
2^{k_2}
2^{k_1}
2^{k_3}
- Batched FRI prover: \(\mathcal{O}(\textsf{\# rows})\)
- Verifier: \(\mathcal{O}(\textsf{\# cols})\)
\(\implies\) recursive prover: \(\mathcal{O}(\textsf{\# cols})\)
zkVM Trace
Op A
Op B
Op C
- Batched FRI prover: \(\mathcal{O}(\textsf{\# rows})\)
- Verifier: \(\mathcal{O}(\textsf{\# cols})\)
- Actual verifier cost: \(\mathcal{O}(\lambda \cdot n \cdot 2^k)\)
-
Solution 1: use multi-variate PCS instead of uni-variate
- Reduces verifier to \(\mathcal{O}(n + k)\)
- However this has two issues:
- Verifier still linear in number of tables
- Height of each table \(n_T\) must be known to
\(\implies\) recursive prover: \(\mathcal{O}(\textsf{\# cols})\)

Jagged Trace
2^k
2^n
Jagged Trace
2^k
2^n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
25
14
15
24
26
27
28
16
17
18
19
20
21
22
23
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
- Sparse trace
- But structured
- Commitment costs: \(2^{k + m}\)
- Non-zero entries: \(M = 2^m\)
- Mapping?
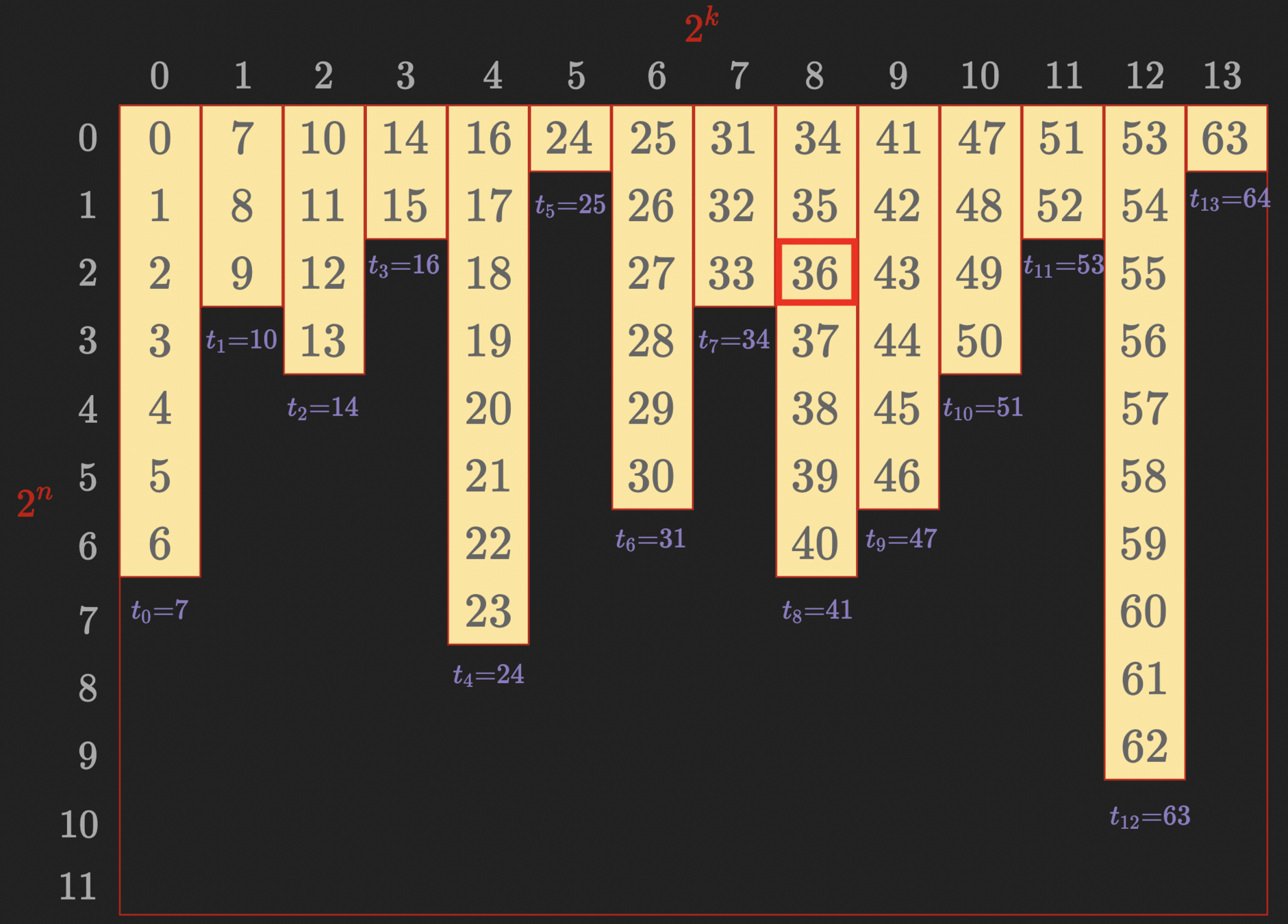
i \in [0, M)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
0
1
2
3
4
5
6
7
8
9
10
11
\implies (x, y)
- Cumulative heights: \(t_y\)
x = i - t_7
\implies y = 8
t_7< i < t_8
t_0\text{=} 7
t_1\text{=} 10
t_2\text{=} 14
t_3\text{=} 16
t_4\text{=} 24
t_5\text{=} 25
t_6\text{=} 31
t_7\text{=} 34
t_8\text{=} 41
t_9\text{=} 47
t_{10}\text{=} 51
t_{11}\text{=} 53
t_{12}\text{=} 63
t_{13}\text{=} 64
Jagged Trace
i \in [0, M)
\implies (x, y)
\implies \ \hat{p} := \textsf{sparse}(\hat{q}, t)
Given oracle access to \(\hat{q},\) can the verifier check:
\hat{q}:
dense representation
\hat{p}:
sparse representation
t:
cumulative heights
\hat{p}(z) \stackrel{?}{=} v
2^k
2^n
0
1
2
3
4
5
6
7
8
9
10
11
12
13
25
14
15
24
26
27
28
16
17
18
19
20
21
22
23
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
0
1
2
3
4
5
6
7
8
9
10
11
12
13
0
1
2
3
4
5
6
7
8
9
10
11
t_0\text{=} 7
t_1\text{=} 10
t_2\text{=} 14
t_3\text{=} 16
t_4\text{=} 24
t_5\text{=} 25
t_6\text{=} 31
t_7\text{=} 34
t_8\text{=} 41
t_9\text{=} 47
t_{10}\text{=} 51
t_{11}\text{=} 53
t_{12}\text{=} 63
t_{13}\text{=} 64
\hat{q}:
dense representation
\hat{p}:
sparse representation
t:
cumulative heights
Jagged PCS
\hat{p}(\textcolor{purple}{z_r, z_c}) \stackrel{?}{=} v
\hat{p}(\textcolor{purple}{z_r, z_c}) := \sum_{\textcolor{grey}{x<2^n}} \sum_{\textcolor{grey}{y < 2^k}}
p(\textcolor{grey}{x, y}) \cdot
\textsf{eq}(\textcolor{grey}{x,} \textcolor{purple}{z_r}) \cdot
\textsf{eq}(\textcolor{grey}{y,} \textcolor{purple}{z_c})
= \sum_{\textcolor{grey}{i<2^m}} \hat{q}(\textcolor{grey}{i}) \cdot
\textsf{eq}\left( \textsf{row}_t(\textcolor{grey}{i}), \textcolor{purple}{z_r} \right) \cdot
\textsf{eq}\left( \textsf{col}_t(\textcolor{grey}{i}), \textcolor{purple}{z_c} \right)
= \sum_{\textcolor{grey}{i<2^m}} \hat{q}(\textcolor{grey}{i}) \cdot
\hat{f}_t(\textcolor{grey}{i}, \textcolor{purple}{z_r}, \textcolor{purple}{z_c})

\stackrel{?}{=} v
Original claim is now reduced to product-sumcheck
\hat{q}:
dense representation
\hat{p}:
sparse representation
t:
cumulative heights
Jagged PCS
= \sum_{\textcolor{grey}{i<2^m}} \hat{q}(\textcolor{grey}{i}) \cdot
\hat{f}_t(\textcolor{grey}{i}, \textcolor{purple}{z_r}, \textcolor{purple}{z_c})

\stackrel{?}{=} v
- Sumcheck rounds: verifier is \(\mathcal{O}(m)\)
- Sumcheck eval:
- \(\hat{q}(\textcolor{purple}{\alpha})\) is given by prover
- \(\hat{f}(\textcolor{purple}{\alpha, z_r, z_c})\): naively, verifier needs \(2^{m + n+ k}\) ops
- Can we do it in \(m \cdot 2^k\)?

Computing \(\hat{f}\)

\hat{f}_t(\textcolor{grey}{i}, \textcolor{purple}{z_r}, \textcolor{purple}{z_c})
= \sum_{\textcolor{grey}{y< 2^k}}\textsf{eq}(y, \textcolor{purple}{z_c}) \cdot
\hat{g}\left(\textcolor{purple}{z_r}, i, t_{y-1}, t_y\right)
\hat{g}\left(\textcolor{purple}{z_r}, i, t_{y-1}, t_y\right)
= 1
- If \(i = \textcolor{purple}{z_r} + t_{y-1}\) and \(i < t_y\) then
- More generally, we define
g(a, b, c, d) = 1
if \(b = a + c\) and \(b < d\).
- Claim: we can compute \(g\) in \(\mathcal{O}(m \cdot 2^k)\)
Read-once Branching Program
- Task is to compute
- \(g(a, b, c, d)\) for all \(a, b, c, d \in \{0, 1\}^m\)
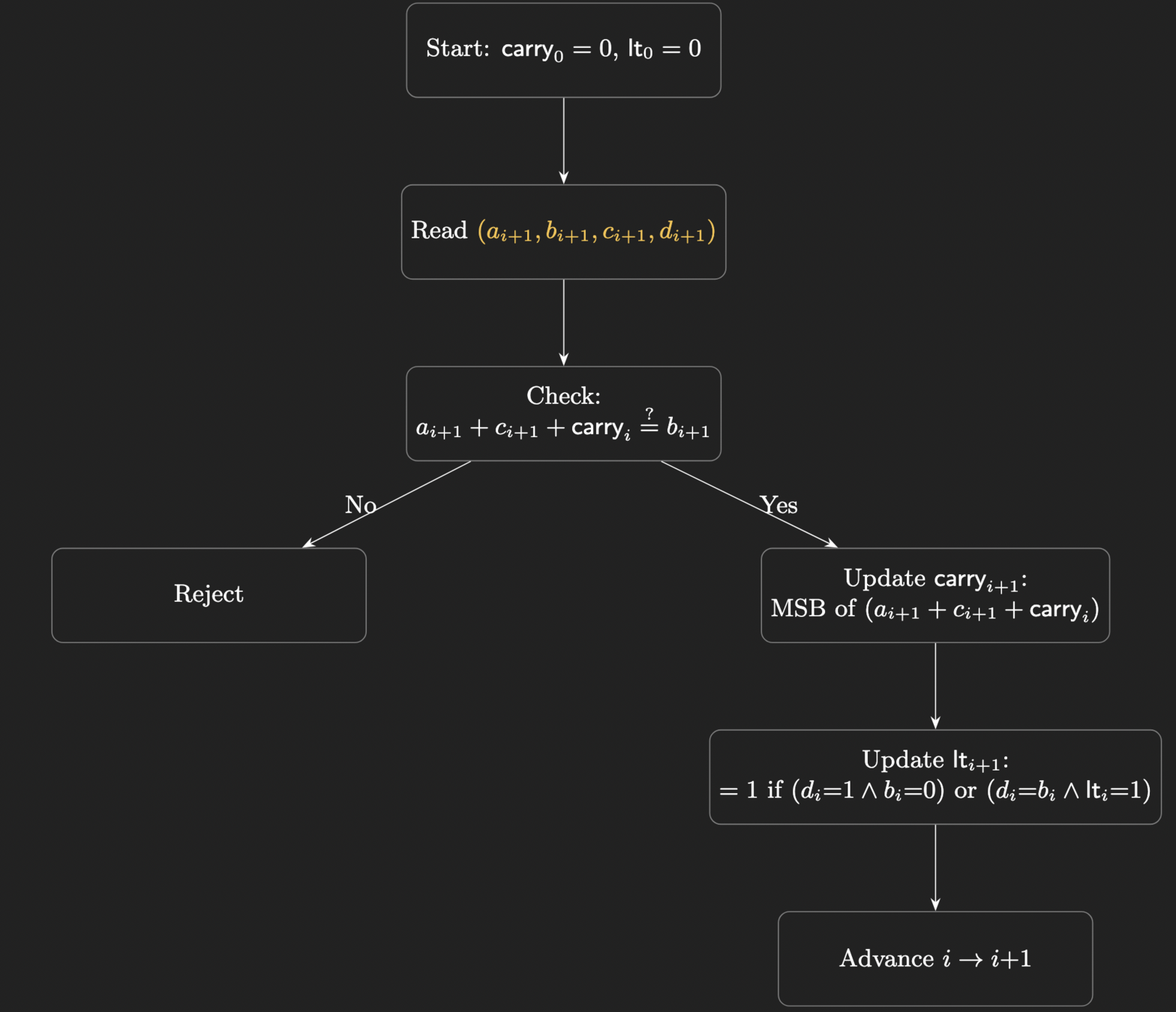
- This is a width-4 ROBP because we use 2 registers
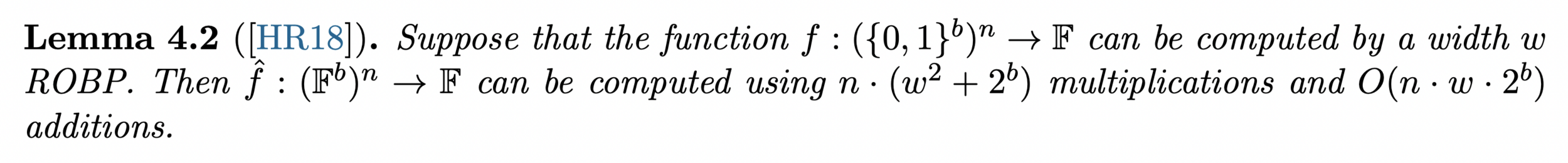
Fancy Jagged
Op A
Op B
Op C
\hat{f}_t(\textcolor{grey}{i}, \textcolor{purple}{z_\textsf{table}}, \textcolor{purple}{z_r}, \textcolor{purple}{z_c})
= \sum_{\textcolor{grey}{y< 2^k}}\textsf{eq}(y, \textcolor{purple}{z_\textsf{table}}) \cdot
\sum_{\textcolor{grey}{u}}\textsf{eq}(u, c_y) \ \cdot
\hat{g}\left(\textcolor{purple}{z_r}, \textcolor{purple}{z_c}, i, c_y, t_{y-1}, t_y\right)
ROBP width-6