Sumcheck over Binary Fields
Journal Club - 10 Jul 2024
Binary Fields
- Binary fields are fields of characteristic \(2\) of the form \(\textsf{GF}(2^n)\)
- When \(n = 1\), we get: \(\textsf{GF}(2) = \{0, 1\} \equiv \mathbb{F}_2\)
- Addition is bitwise XOR and multiplication is bitwise AND
- When \(n = 2\), the field \(\textsf{GF}(2^2)\) is a degree-2 extension of \(\textsf{GF}(2)\)
- Let \(m(x) = x^2 + x + 1\) be the irreducible polynomial
- Any polynomial \(p(x)\) over \(\mathbb{F}_2\) when divided by \(m(x)\) gives the remainder
- Resulting field is \(\textsf{GF}(2^2)\)
- Towers of binary fields
1x + 0
0x + 0
0x + 1
1x + 1
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
Binary Fields
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}
\textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1} \
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1}
\vdots
\vdots
Binary Fields
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}
\textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1} \
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1}
\vdots
\vdots
Binary Fields
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}
\textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1} \
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1}
\vdots
\vdots
Binary Fields
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}
\textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1} \
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1}
\vdots
\vdots
Binary Fields
\textsf{GF}(2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^2)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^4)
\ \xrightarrow[\text{extension}]{\text{deg-2}} \
\textsf{GF}(2^8)
\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}
\textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{grey}{0}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{grey}{0}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{grey}{0}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{grey}{0}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y +\textcolor{lightgreen}{1}x + \textcolor{grey}{0}
\textcolor{lightgreen}{1}xy + \textcolor{lightgreen}{1}y + \textcolor{lightgreen}{1}x + \textcolor{lightgreen}{1}
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1} \
\textcolor{lightgreen}{1} \
\textcolor{grey}{0} \
\textcolor{lightgreen}{1}
\vdots
\vdots
- Addition is bitwise XOR
- Multiplication?
a \cdot b
=(a_{\textit{h}}x + a_{\textit{l}}) \cdot (b_{\textit{h}}x + b_{\textit{l}})
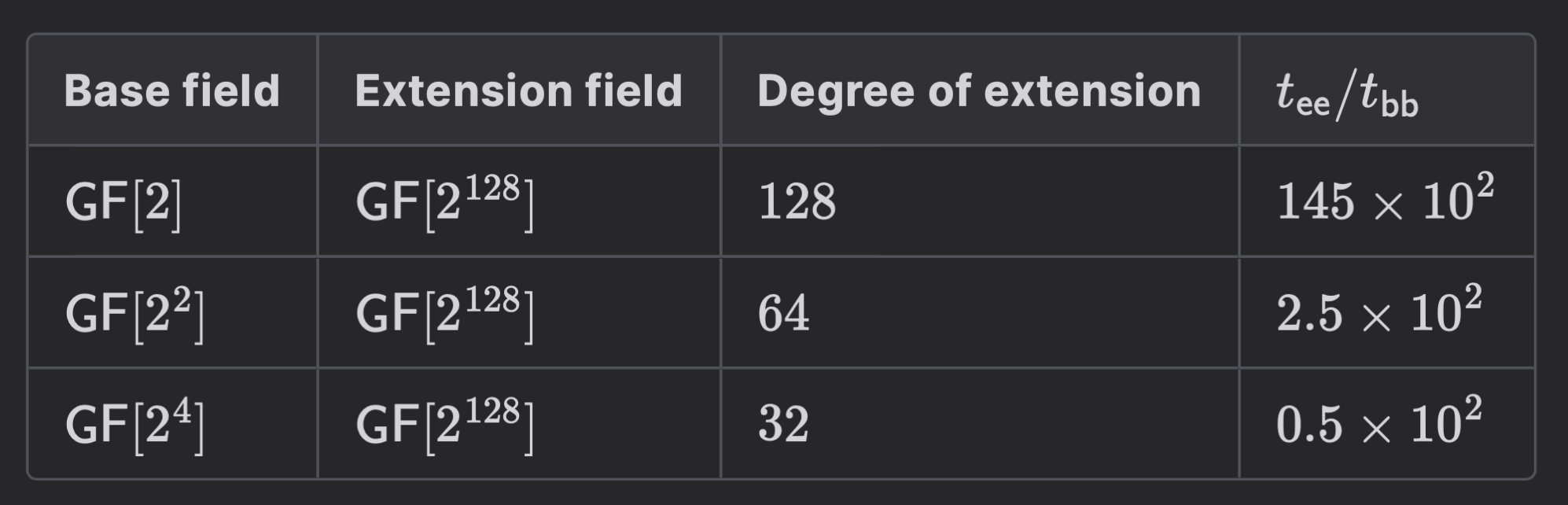
Why Sumcheck over Binary Fields?
p(x) := p_1(x) \cdot p_2(x) \cdots p_d(x)
- Binius enables efficient SNARKs over binary fields
- Fast commitment scheme + sumcheck based IOPs
- Commitment part is so fast that sumcheck could become the bottleneck
- We need sumcheck to prove (multilinear) polynomial relations like
- Sumcheck round polynomial in round \(i\)
s_i(c) := \sum_{x \in \{0, 1\}^{\ell - i}} p(r_1, r_2, \dots, r_{i - 1}, c, x)
= \sum_{x \in \{0, 1\}^{\ell - i}} \prod_{j=1}^{d} p_j(r_1, r_2, \dots, r_{i - 1}, c, x)
Product of extension-field elements
Why Sumcheck over Binary Fields?
s_i(c) := \sum_{x \in \{0, 1\}^{\ell - i}} p(r_1, r_2, \dots, r_{i - 1}, c, x)
= \sum_{x \in \{0, 1\}^{\ell - i}} \prod_{j=1}^{d} p_j(r_1, r_2, \dots, r_{i - 1}, c, x)
Product of extension-field elements

Product of Linear Polynomials
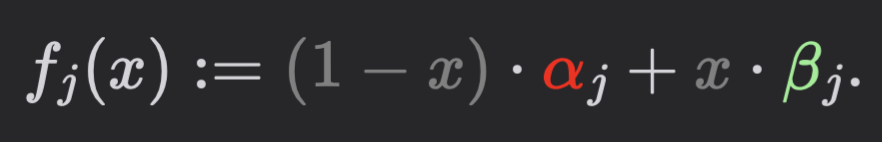
- Let \(f_1, f_2, \dots, f_d\) be linear polynomials s.t.
- Using school-book multiplication
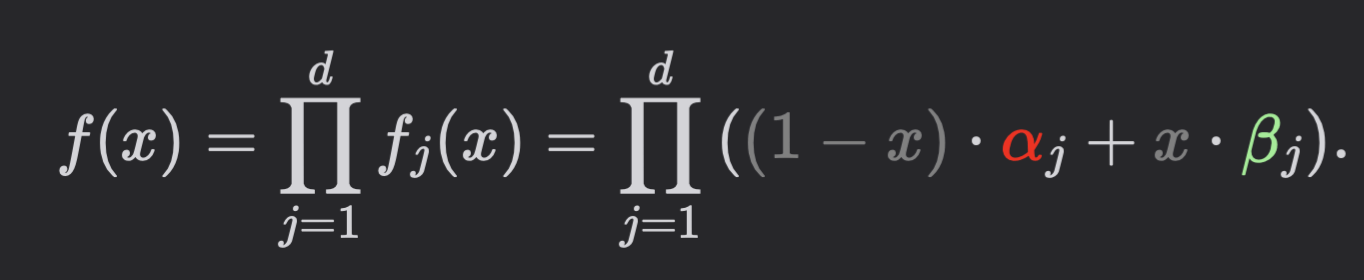

\implies (d - 1) \cdot 2^d \ \textsf{bb}
Efficient Product of Linear Polynomials
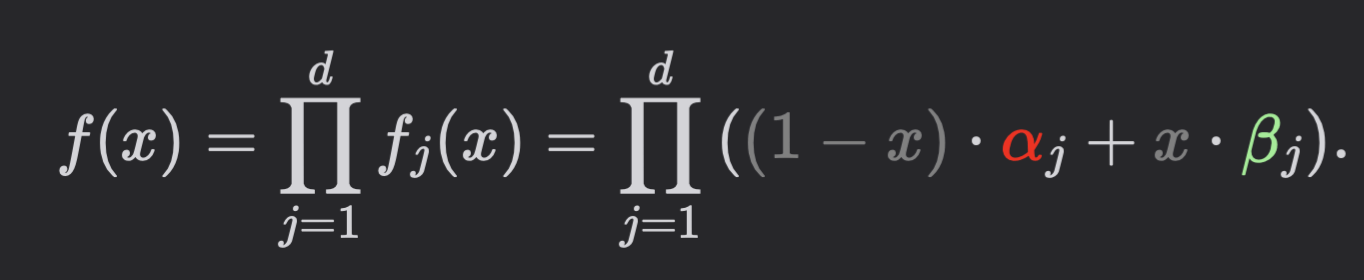
- Degree of \(f\) is \(d\). To compute \(f(x)\):
- Evaluate each \(f_j\) on \(d + 1\) points \(\{e_0, e_1, \dots, e_d\}\)
- Compute point-wise multiplication on all \(d\) points to get \([f(e_0), \dots, f(e_d)]\)
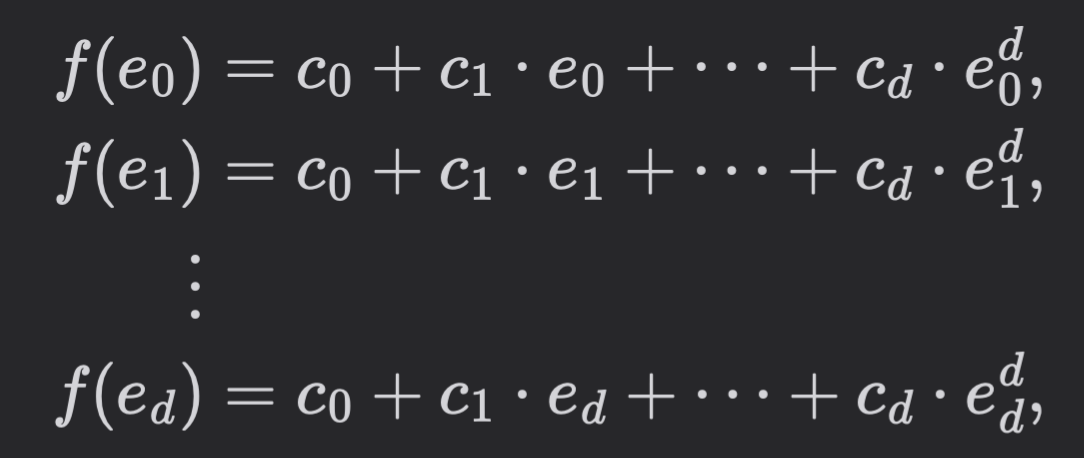

\implies

\implies
\implies (d - 1) \cdot (d + 1) \ \textsf{bb}
Efficient Product of Linear Polynomials
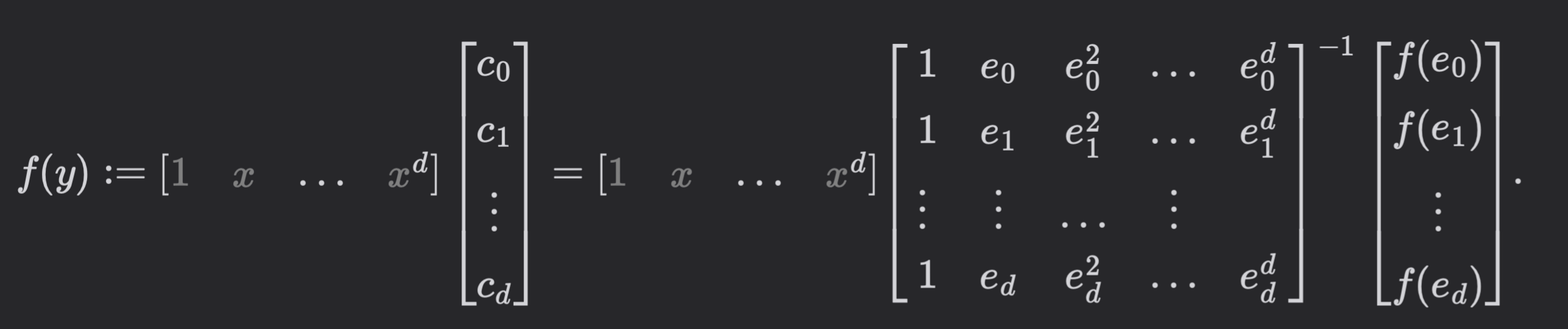

Schoolbook method
Toom-Cook method
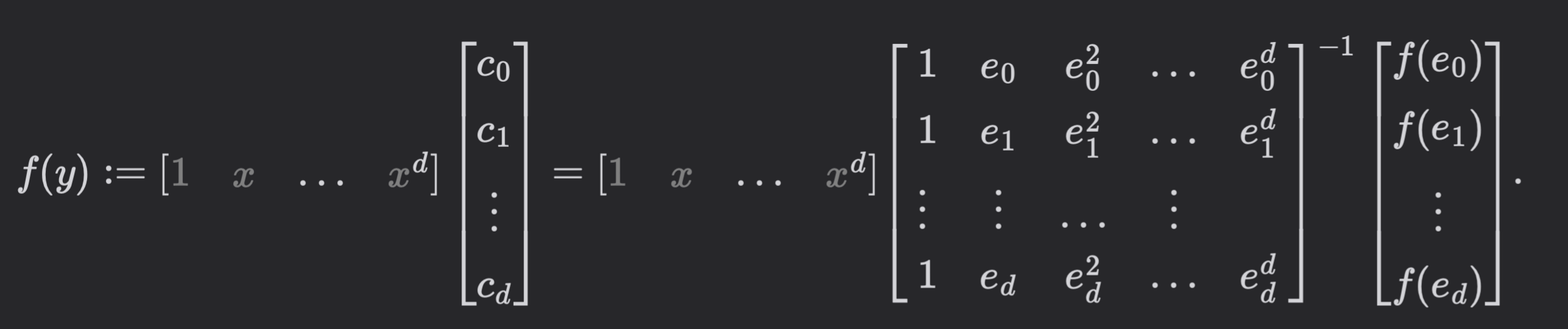
\implies (d - 1) \cdot (d + 1) \ \textsf{bb}
\implies (d - 1) \cdot 2^d \ \textsf{bb}
Efficient Product of Linear Polynomials

Schoolbook method
Toom-Cook method
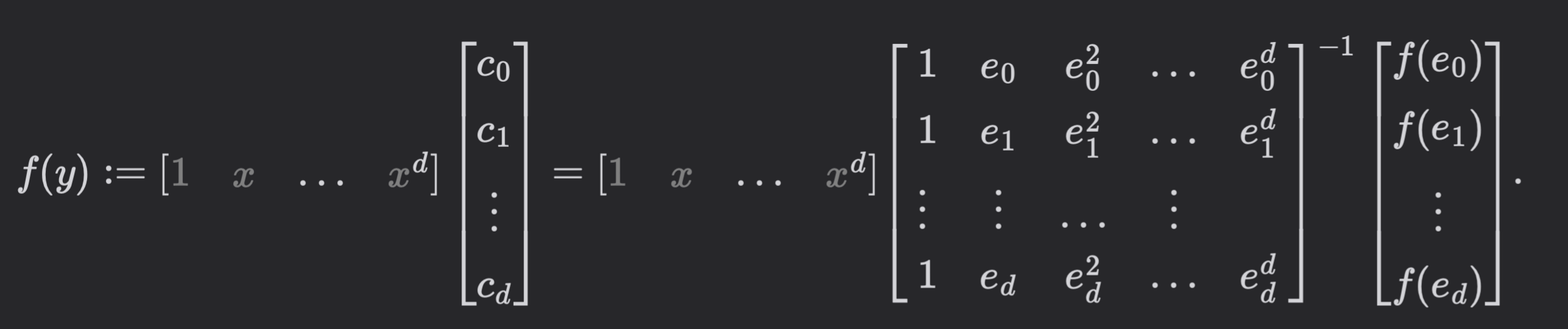
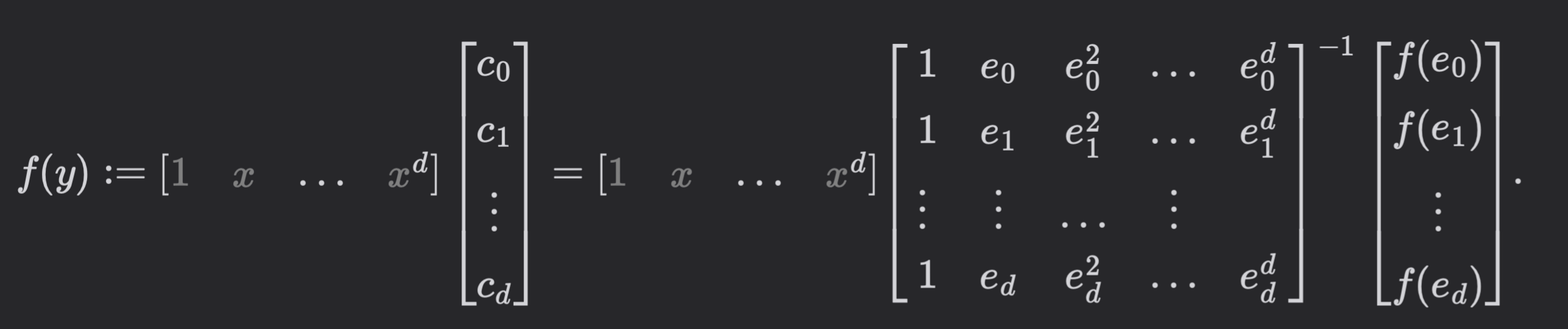
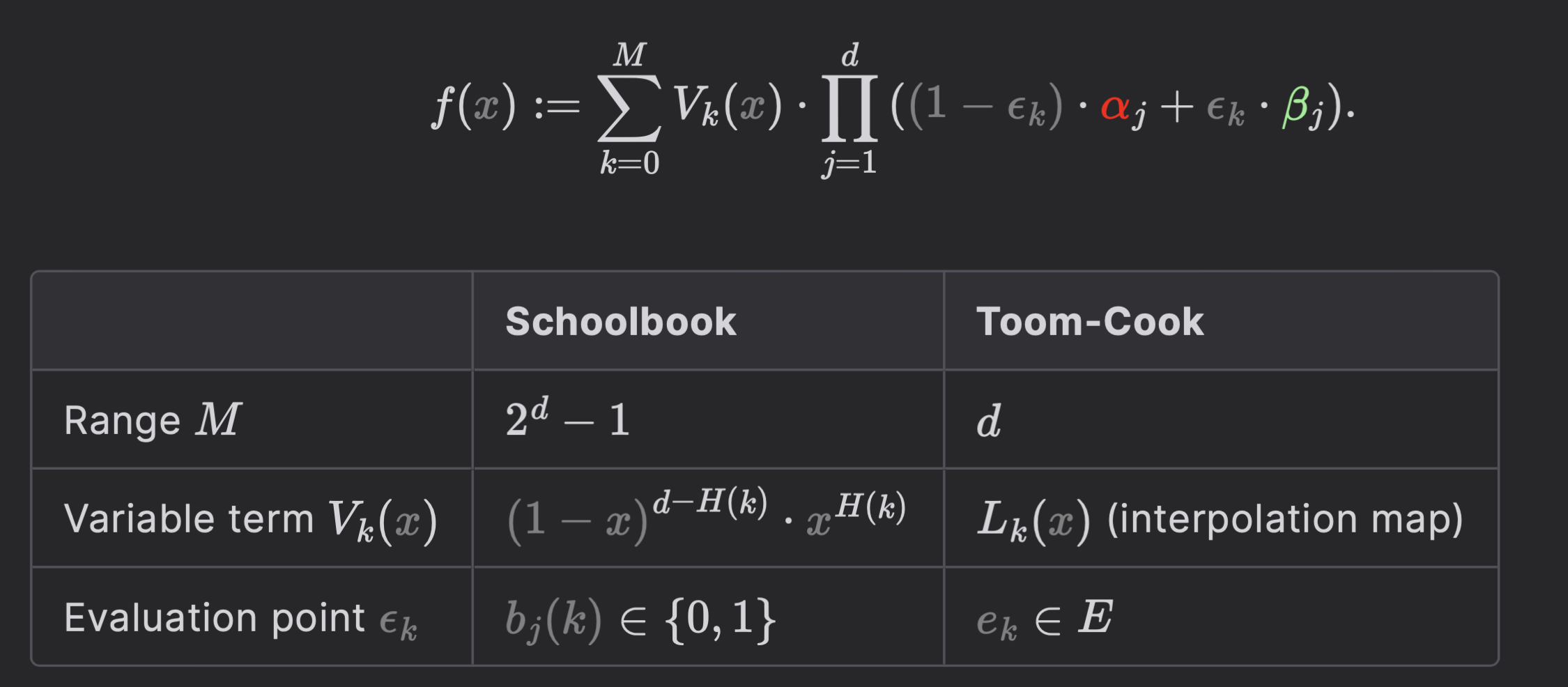
Back to Sumcheck
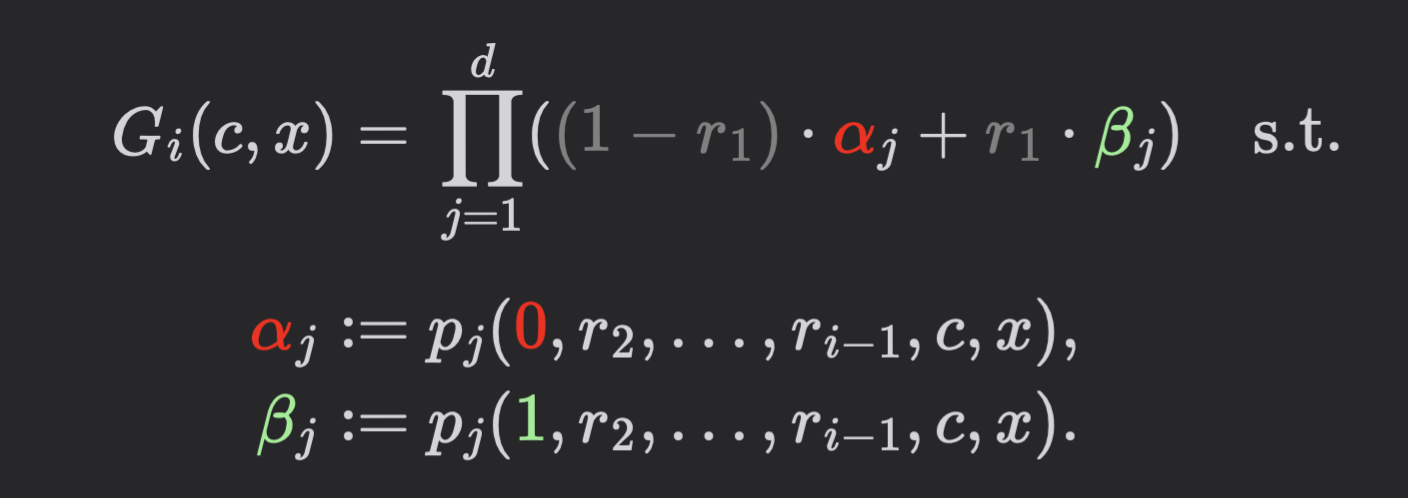
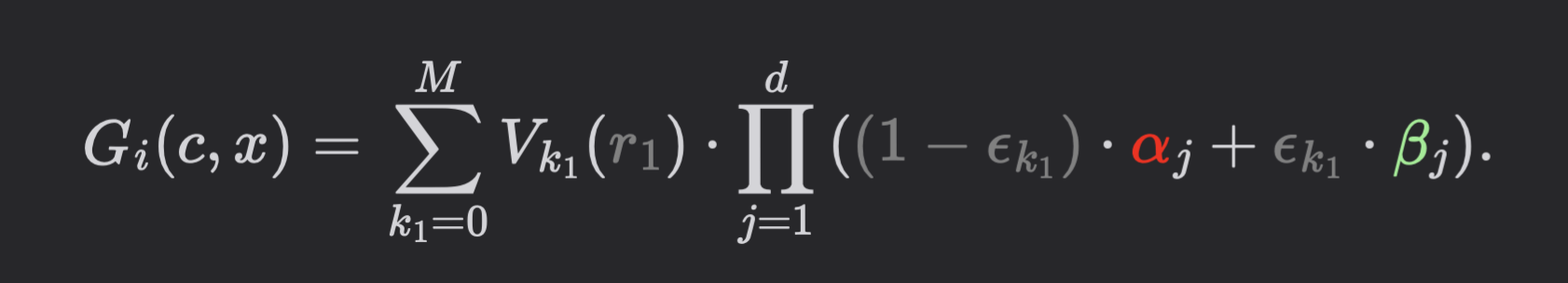
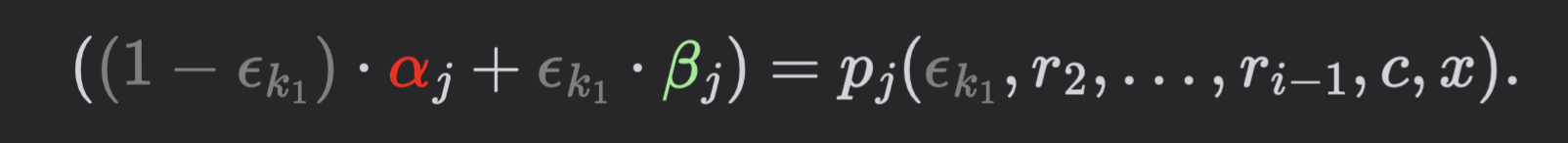
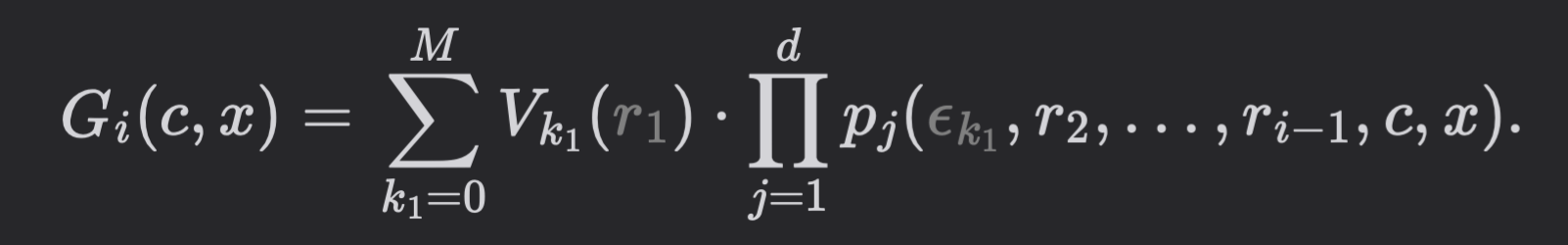
\implies
\implies
Back to Sumcheck
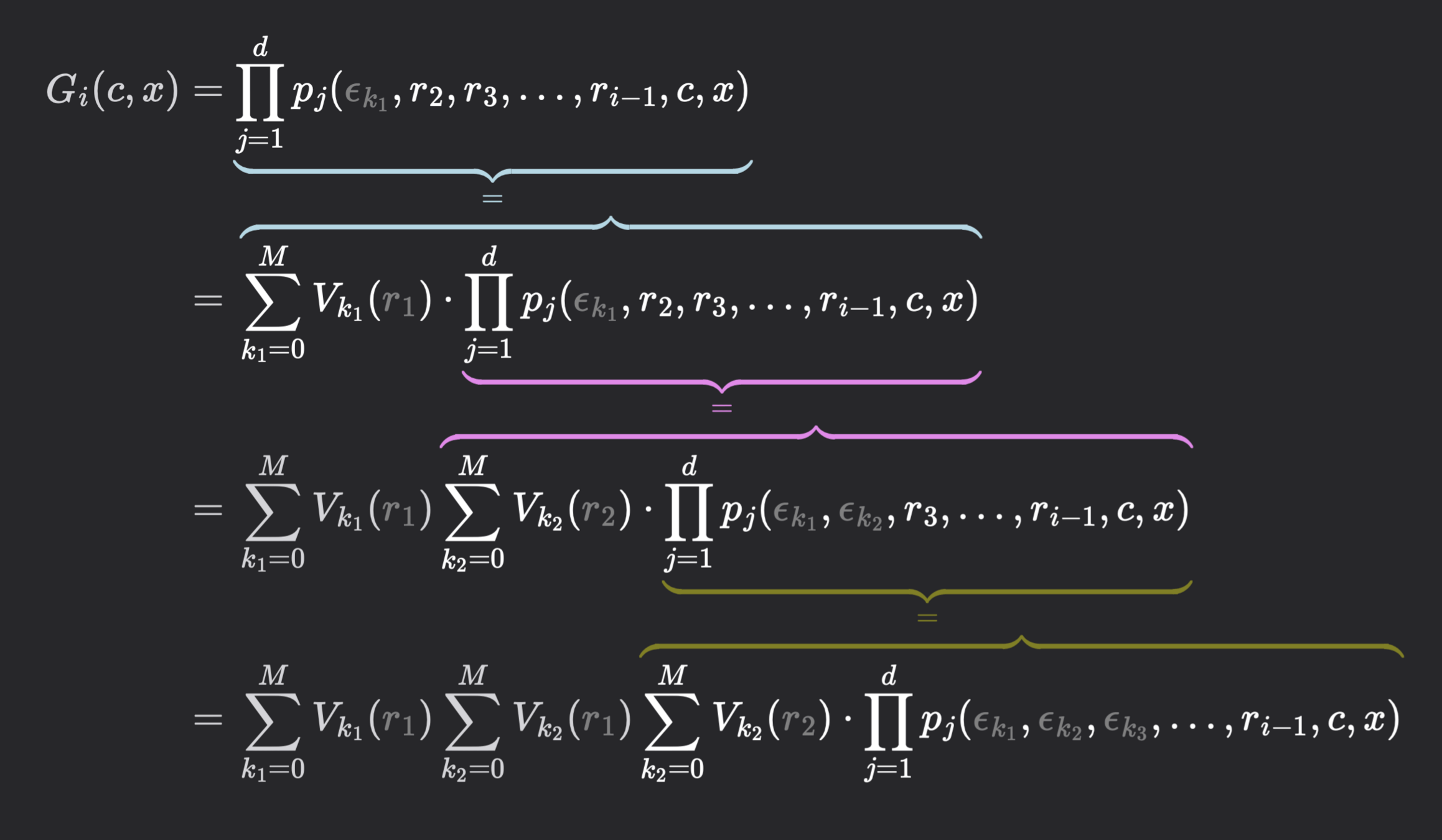
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
(d + 1)^t
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
(d + 1)^t
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
e_1[0]
e_1[1]
e_1[2]
e_1[3]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
\left[e_2[0] \ \dots \ e_2[2^{\frac{n}{2}}\right]
(d + 1)^{t-1}
e_1[4]
e_1[5]
e_1[6]
e_1[7]